The movement of fluids can be described by the Navier-Stokes equations, known for the inexistence of an analytical solution to date. Therefore a numerical approach is considered in most cases when
the problem is more or less complex.
$$ \frac{\partial c}{\partial t}=-u_{x}(x, y, t) \frac{\partial c}{\partial x}-u_{y}(x, y, t) \frac{\partial c}{\partial y}+D\left(\frac{\partial^{2} c}{\partial x^{2}}+\frac{\partial^{2} c}{\partial y^{2}}\right)+S(x, y, t)$$
Looking at the equation above, it is noted that the concentration \(c\) of the pollutant, that is to say the ratio of its mass per unit volumne relative to the density (weight to volume) of the medium in which it is dispersed, is governed by three key parameters: advection, diffusion and source of pollutant.
The first two terms to the right of the equation represent the advective terms. The advection is the transport of a quantity, here the pollutant concentration, caused by the movement of its surroundings, here described by the speed of the atmospheric air.
Then, the third term is used to describe the diffusion of the fluid using the diffusion coefficient \(D\). The diffusion is the tendency of a natural system to make uniform the chemical potential of each chemical species it contains. In other words, the chemical species range from a high concentration medium to a low concentration environment.
Finally, the last term takes into account the source \(S\) of the pollutant. The source is used to describe the spatial (x, y) and temporal profile of the element emitting the pollutant.
Suppose that a foundry, placed in the center of the simulation, constantly emits a gas containing arsenic for \(t = 2.5\). The boundary conditions are such that the fluid reaching the left end is then found at the right end, the same for the top and bottom.
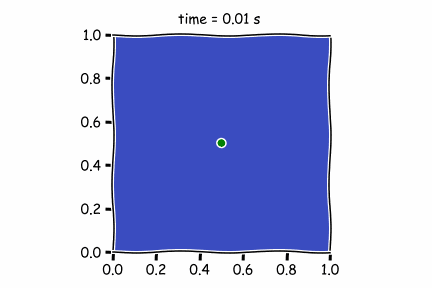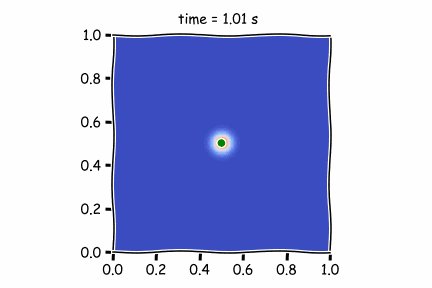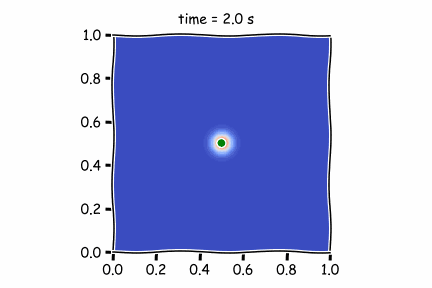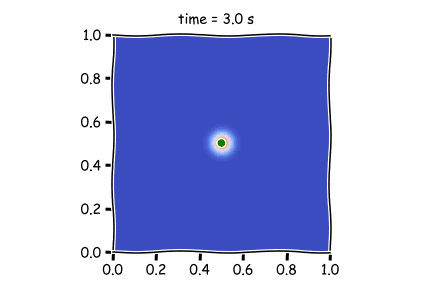
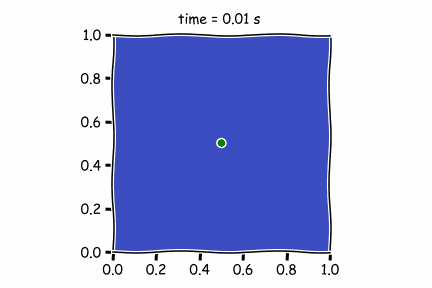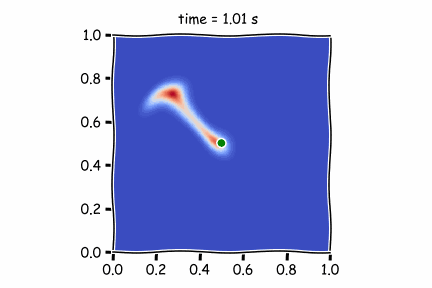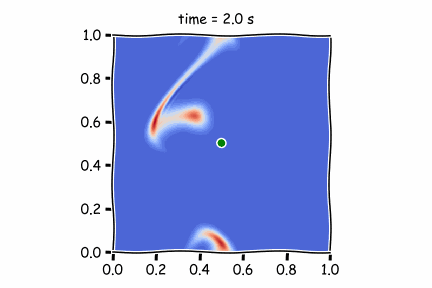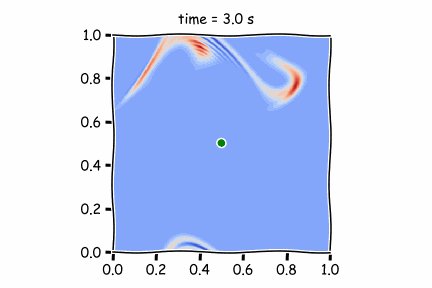
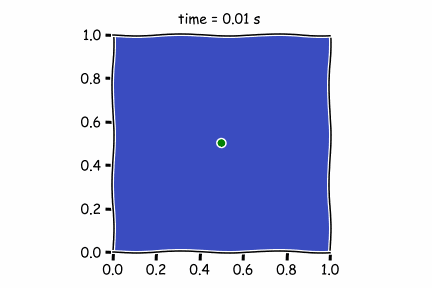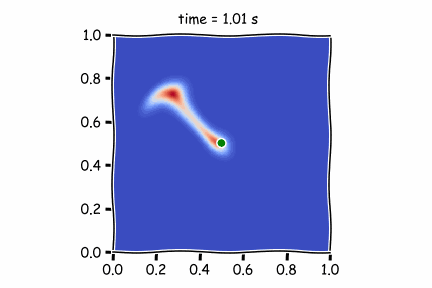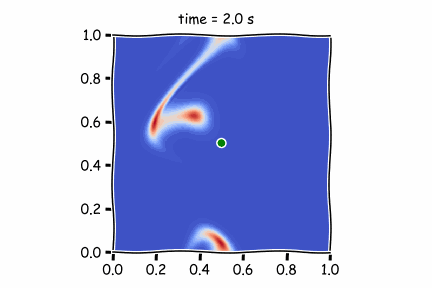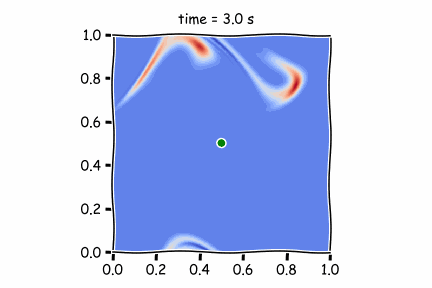
Figure 1 : Diffusif term only
Figure 2 : Advectif terms only
Figure 3 : Both of them
In the first figure, there is only the diffusive term. As it is not very high (high Peclet Number), the pollutant is not moving far from its original position.
Then, by using only the advective terms (Figure 2), we see that the pollutant is strongly pushed by the atmospheric air and is found to be diluted. Taking into account wind speed and diffusion, as in Figure 3, the fluid moves faster.
Moral of the story: you should therefore not stay close to the source if there are no winds, at the risk of catching cancer!